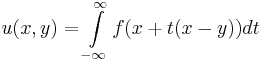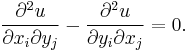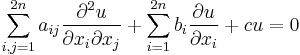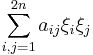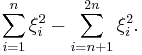John's equation

John's equation is an ultrahyperbolic partial differential equation satisfied by the X-ray transform of a function. It is named after Fritz John.

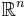Given a function f:\mathbb{R}^n \rightarrow \mathbb{R} with compact support the X-ray transform is the integral over all lines in \mathbb{R}^n. We will parameterise the lines by pairs of points 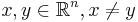x,y \in \mathbb{R}^n, x \ne y on each line and define u as the ray transform where

u(x,y) = \int\limits_{-\infty}^{\infty} f( x %2B t(x-y) ) dt

then u satisfies John's equation

\frac{\partial^2u}{\partial x_i \partial y_j} - \frac{\partial^2u}{\partial y_i \partial x_j}=0.

In three dimensional x-ray computerized tomography John's equation can be solved to fill in missing data, for example where the data is obtained from a point source traversing a curve, typically a helix.

More generally an ultrahyperbolic partial differential equation (a term coined by Richard Courant) is a second order partial differential equation of the form

\sum\limits_{i,j=1}^{2n} a_{ij}\frac{\partial^2 u}{\partial x_i \partial x_j} %2B \sum\limits_{i=1}^{2n} b_i\frac{\partial u}{\partial x_i} %2B cu =0

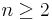where n \ge 2, such that the quadratic form

\sum\limits_{i,j=1}^{2n} a_{ij} \xi_i \xi_j

can be reduced by a linear change of variables to the form

\sum\limits_{i=1}^{n} \xi_i^2 - \sum\limits_{i=n%2B1}^{2n} \xi_i^2.

It is not possible to arbitrarily specify the value of the solution on a non-characteristic hypersurface. John's paper however does give examples of manifolds on which an arbitrary specification of u can be extended to a solution.

References